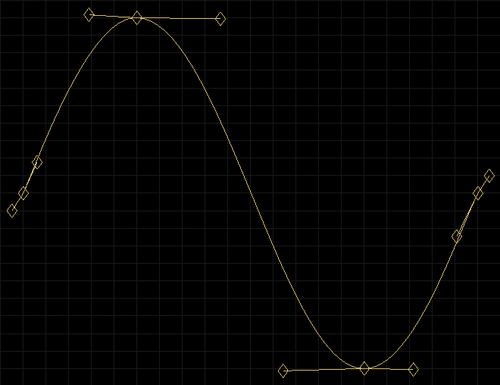
Sine waveform approximated with 3 Bezier curves. We say approximated because only the sine function can produce an accurate sine curve. And that, in an abstract mathematical world! If you use a sine function on a computer, its accuracy will depend on the largest and the smallest numbers you can represent on that computer. The greater this range, more accurate the sine function. But that is not the end of the story. The nature of digital audio is such that the digital sine waveform will be more accurate at low frequencies and very inaccurate at very high frequencies
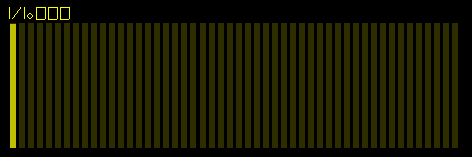
Fast Fourier Transform (FFT) of the Bezier sine waveform. Only the fundamental frequency is present. This is an important result because it doesnt matter if we use Bezier curves or the sine function to make the sine waveform, the FFT is going to be the same and so we will hear the same sound.
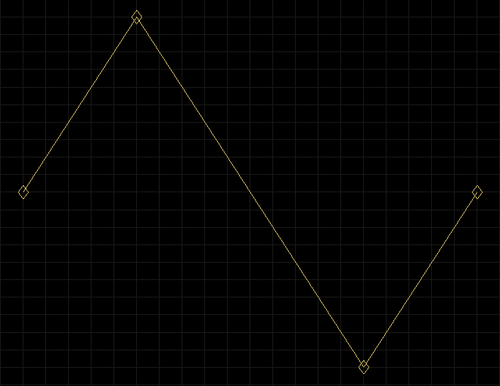
Triangle waveform made with 3 Bezier curves. The handles of a Bezier curve allow you to sculpt its shape. But when they lie on top of the control points like they do here, they lose their power. You end up with your classic waveform.
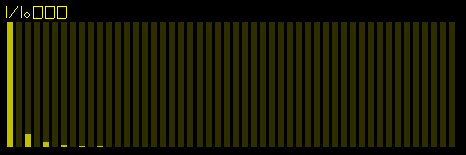
Fundamental frequency is dominant with a sprinkling of first few odd harmonics.
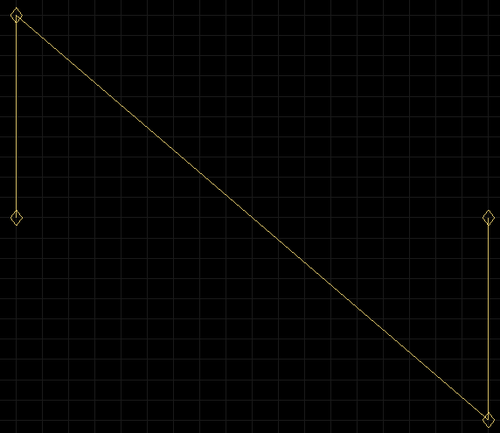
Pulse waveform. Handles on top of control points.
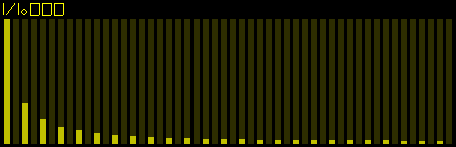
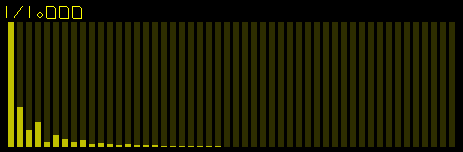
Only odd harmonics are present.
Sawtooth waveform. Handles on top of control points.
Both odd and even harmonics are present.
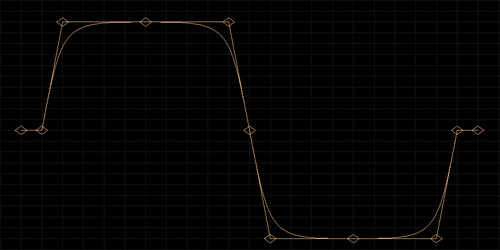
Cross between a triangle and pulse waveform. This sounds a lot softer than the pulse but much louder than the triangle.
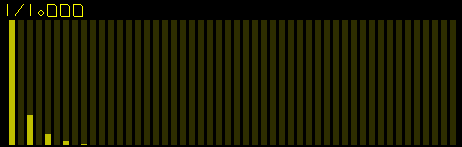
Like the triangle waveform, only the first few odd harmonics are present but these are stronger. Absence of higher odd harmonics presents a softer sound.
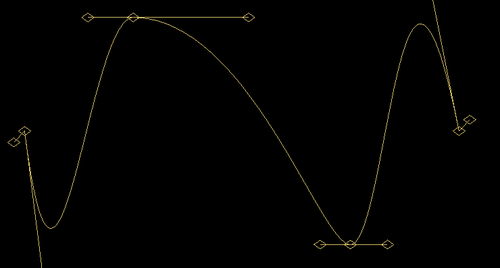
A Bezier waveform is a collection of Bezier curves. This waveform has 4 control points (aka Vertices) connected by 3 Bezier curves. 8 handles (aka Tangents) - 2 for each vertex - are available to sculpt your waveform.
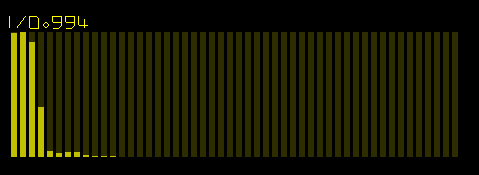
The FFT of each Bezier waveform is unique like a fingerprint. It has its own sound.
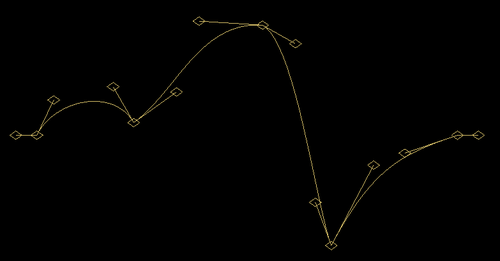
A Bezier waveform can have as many points as you like, can be as long as you like, as tall as you like and you can have as many of them as you like. No limits.
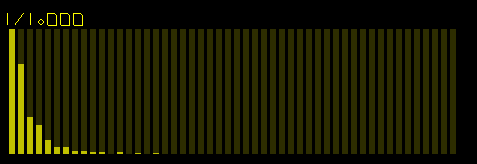
Took a pulse waveform with a 25% / 75% pulse profile and gave it a Bezier twist.
DIN Is Noise is Copyright (c) 2006-2023 Jagannathan Sampath.
DIN Is Noise for GNU+Linux, FreeBSD and NetBSD is Free Software.
SSL Report
See also: https://dinisnoise.org/pics/